Manchmal trifft Angebot direkt auf Nachfrage: Ich hatte in Edinburgh die Gelegenheit, direkt mit Chris Sangwin, dem „Erfinder“ von STACK, vor einem Rechner zu sitzen und mir die neuesten Funktionalitäten zeigen zu lassen – die dann tatsächlich auch unsere Fehlermeldungen beseitigen sollten, die seit dem letzten Update aufgekommen waren. Es geht um die Fehlermeldung „Es fehlen Tests oder Varianten“ in der Vorschau zu STACK-Fragen (wie in der Abbildung gezeigt) – also um den technischen Teil des Anlegens von Testfällen und Varianten. Für Erfahrenere gibt es hier direkt einen Screencast (Länge 4:11) zur Durchführung.

Fragevarianten in STACK
Ein bisschen Theorie zu STACK vorweg: STACK steht für System for Teaching and Assessment using a Computer algebra Kernel. Hinter dem System steckt eine Computer Algebra (in diesem Fall Maxima), die spezielle, für STACK entwickelte Generatoren für Zufallszahlen nutzt. Damit lassen sich randomisierte Tests erstellen. Um diese Zufallszahlen nachvollziehbar zu halten (auch zu Dokumentationszwecken), starten sie deterministisch stets vom gleichen Startwert.
In der Aufgabe selbst muss daher hinterlegt werden, bei welcher Variable genau überprüft werden soll, ob bestimmte Varianten schon „gewürfelt“ wurden. Das erfolgt im Feld Aufgabenhinweis. Hier ist es wichtig, die randomisierte Variable aus dem Aufgabentext einfügen. Als anschauliches Beispiel: Wenn eine quadratische Funktion f gewürfelt wird mit zwei zufällig vorgebenen Nullstellen, dann ist es für die Funktion f egal, ob die erste Nullstelle den Wert 1 und die zweite den Wert 2 oder umgekehrt – es handelt sich beide Male um dieselbe Funktion. STACK erkennt diese algebraische Identität und generiert entsprechend nur eine Aufgabe aus beiden „Würfen“ (wenn korrekt aufgesetzt…).
Ist die Funktion in den Aufgabenvariablen als fkt bezeichnet, so wird sie als {@fkt@} in der Aufgabenstellung aufgerufen und muss mit dieser Syntax auch im Aufgabenhinweise erscheinen (also nicht nur als fkt!). In der Beispielabbildung ist eine Funktion f gegeben (die in den Variablen als p wie Polynom definiert wurde) und gesucht ist die Ableitung f‘, in dem Fall also die Musterlösung ta (teacher’s answer). Der Aufgabenhinweis sieht also folgendermaßen aus:

Die nächsten beiden Aspekte werden in dem Fenster eingestellt, das erscheint, wenn man auf die Fehlermeldung klickt bzw. bei einer korrigierten Variante auf:

Die Seite sieht dann so aus:
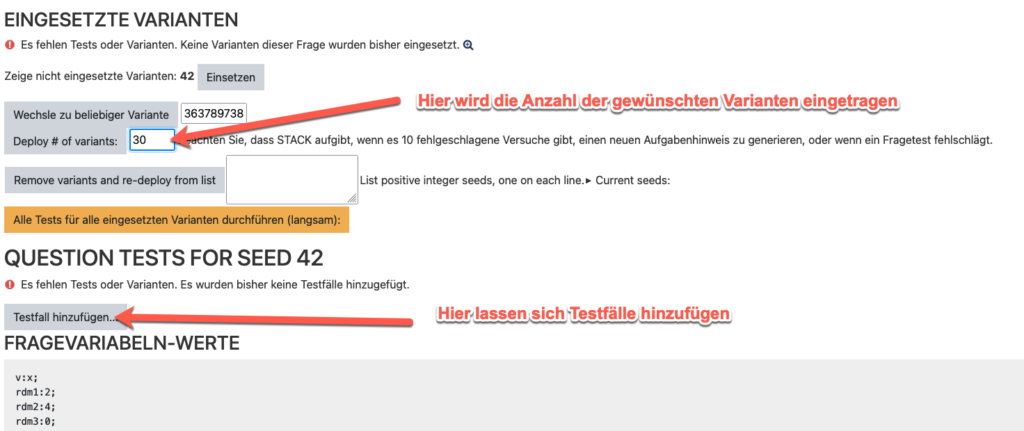
Testfälle erstellen für die Überprüfung des Rückmeldebaums
STACK erlaubt es, Testfälle anzulegen, um den Rückmeldebaum zu überprüfen. Für komplizierte Bäume empfiehlt es sich, entsprechend Testfälle für das Durchlaufen aller Pfade anzulegen. Um die Fehlermeldung zu beseitigen, genügt es, den einfachsten Testfall automatisch anlegen zu lassen, um zu prüfen, dass die Musterlösung volle Punktzahl ergibt.

Fragevarianten anlegen
Weiterhin müssen die Varianten, die eingesetzt werden sollen, auch erzeugt werden. Dazu kann eine beliebige Anzahl von Zufallszahlen von wählbaren Startwerten aus erzeugt werden. Erfolgen mehr als 10 gleiche Varianten, bricht STACK ab. Dieser Schritt lässt sich unabhängig vom Erstellen der Testfälle durchführen. Aus meiner Sicht bietet es sich an, die Varianten erst nach dem Errstellen der Testfälle vorzunehmen, da dann automatisch der Test auch für die Varianten durchlaufen wird.
Angezeigt wird für jeden Fall das, was im Aufgabenhinweis angegeben wurde. Nach Erzeugung lassen sich auch unerwünschte Varianten entfernen. Für das Beispiel der Funktion f mit Ableitungsfunktion f‘ ergibt sich dann folgendes Bild:

